Venn Diagram

What is a Venn Diagram?

A Venn diagram is a schematic representation of the elements in a set or a group. It is a diagram that shows all the possible logical relationships between a finite assemblage of sets or groups. It is also referred to as a set diagram or logic diagram.

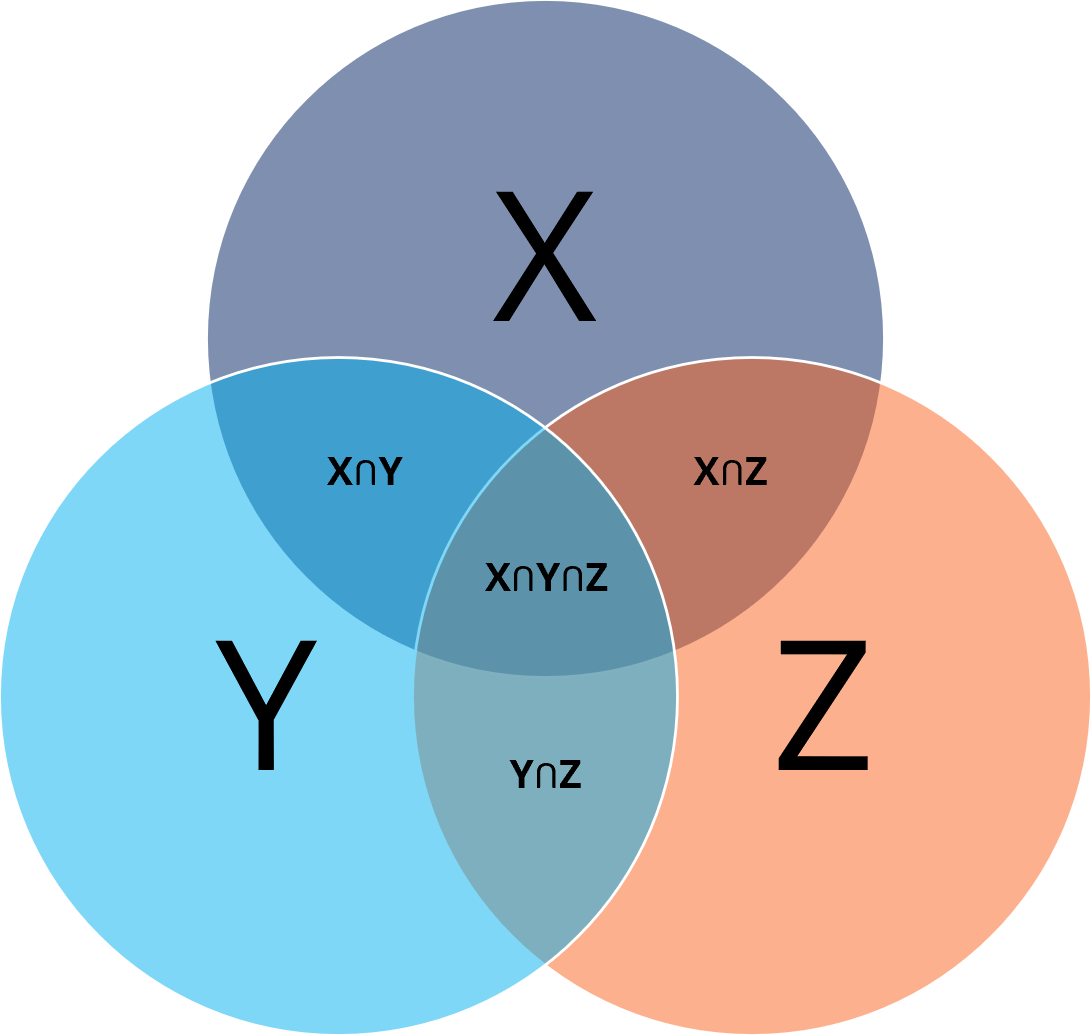
A Venn diagram uses multiple overlapping shapes (usually circles) representing sets of various elements. It aims to provide a graphical visualization of elements, highlighting the similarities and differences between them.

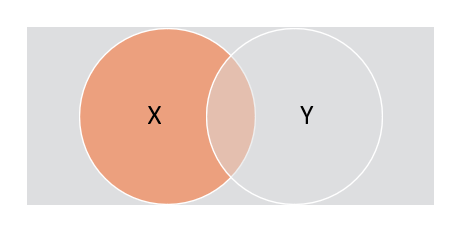
They are mainly used in set theory and also to illustrate relationships between elements in various areas, such as statistics, logic, probability, linguistics, business, and computer science. An example of a Venn diagram above shows three sets labeled X, Y, and Z and the corresponding relationships between elements in each set.

Venn diagrams provide a powerful visual display of data, commonly used in presentations and business and scientific reports. They are related to Euler diagrams, which only differ in that they do not illustrate a set if there are no elements present.

Venn Diagrams Symbols

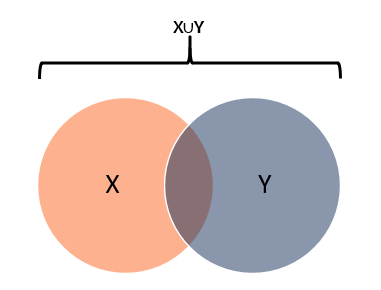
Union (∪): Represents the union of all sets – i.e., the universe of all elements within X and Y sets.

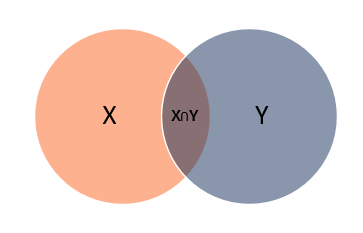
Intersection (∩): Represents all elements shared or common within the selected sets or groupings. Intersection represents shared elements (in the middle) within sets X and Y.

Complement (X^C): Represents whatever is not represented in a particular set; in this case, everything not in set X. An equation to illustrate the complement of X is X^C = U/A, where U represents a given universe of elements. The diagram below shows the absolute complement of X in U – i.e., everything in the universe except for X (grey area).

History of Venn Diagrams

The Venn diagram concept was established by British mathematician and logician John Venn. It was first published in his 1980 journal titled “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings.” However, the development of Venn diagrams can be traced back to the 1200s through philosopher and logician Ramon Llull, who drew similar types of diagrams.

There are various other logicians who also drew similar diagrams, but the closest diagrams that resemble Venn diagrams were first drawn by Leonard Euler in the 1700s. He drew what he defined as Euler diagrams. John Venn referenced Euler in his diagrams, which he first described as Euler circles.

The term Venn diagram was first published by Clarence Irvine Lewis in his 1918 book, “A Survey of Symbolic Logic.” Mathematicians and logicians continued to improve the diagrams in the 19^th and 20^th centuries to show clearer and more complex relationships using more sets. Venn diagrams were adopted in various disciplines and complexities aided by evolving technology and the use of computers.

Using Venn Diagrams

As highlighted above, Venn diagrams are used in several ways to show relationships between various set elements. Below are examples of uses of Venn diagrams.

Example 1: Subjects Taken by Students

A study is being done at a school on students who take the subjects mathematics and economics. There are 12 students who attend both classes and 2 students who do not take either of the subjects.

Mathematics ∪ Economics: {Charlotte, Lewis, Olivia, Eddie, Sophia, Liam, Brea, Avery, Noah, Isabella, Mia, Eric}. The illustration is below:

The union of the two subjects is the universe of all students who take both classes – i.e., 12 students.

Mathematics ∩ Economics: {Sophia, Liam, Brea, Avery, Noah}

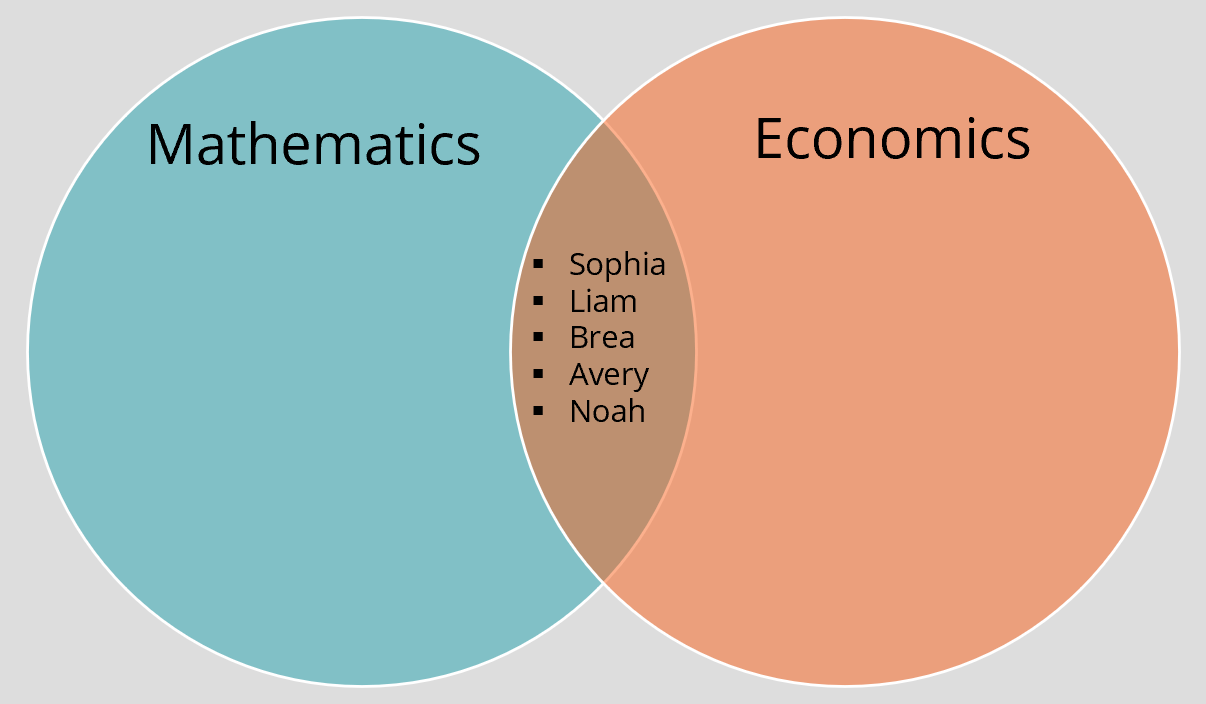
The above shows the intersection of students who take mathematics and economics. These are students who take both subjects but do not take only one of the subjects.

Mathematics^C: {Isabella, Mia, Eric, Joe, Nina}

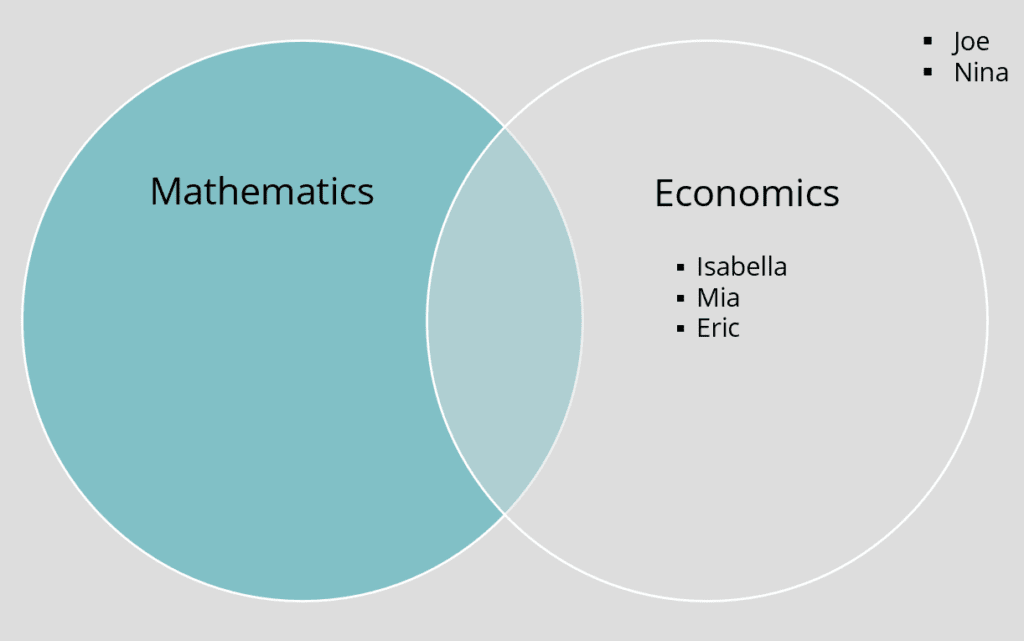
The complement of mathematics represents all students that do not take mathematics. These include students that take economics but not mathematics and students that do not take either subject (grey area).

Example 2: Collective Investment Funds

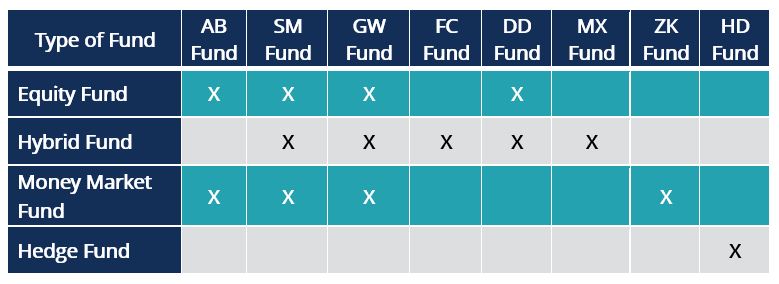
The table above compares eight investment funds in terms of the types of funds that each fund operates. There are different types of funds under consideration, notably equity fund, money market fund, hybrid fund (i.e., a mixture of equity and money market instruments), and a hedge fund. The eight investment funds operate one or more of these fund types.

Through distinct color-coding, the Venn diagram clearly shows where each fund lies. A few observations on the above chart are discussed below:

• The universe of all investment funds save for hedge funds is represented by the following notation:

Equity Fund ∪ Hybrid Fund ∪ Money Market Fund: {AB Fund, SM Fund, GW Fund, ZK Fund, FC Fund, MX Fund, DD Fund}

• Only two funds {SM Fund, GW Fund} have all three fund types save only a hedge fund. This is represented by the following notation:

Equity Fund ∩ Money Market Fund ∩ Hybrid Fund

• The AB Fund is the only fund that has both equity and money market funds only. This is represented by the following notation:

Equity Fund ∩ Money Market Fund

• The DD Fund is the only fund that has both equity and hybrid funds only. This is represented by the following notation:

Equity Fund ∩ Hybrid Fund

• The ZK Fund is the only fund without other fund types save for money market fund.
• The FC Fund and MX Fund are the only funds without other fund types save for hybrid fund.
• There are no funds that have money market and hybrid funds exclusively.
• There are no funds that have equity funds exclusively.
• The HD Fund is the only fund operating a hedge fund, and it does not operate any other type of investment fund.

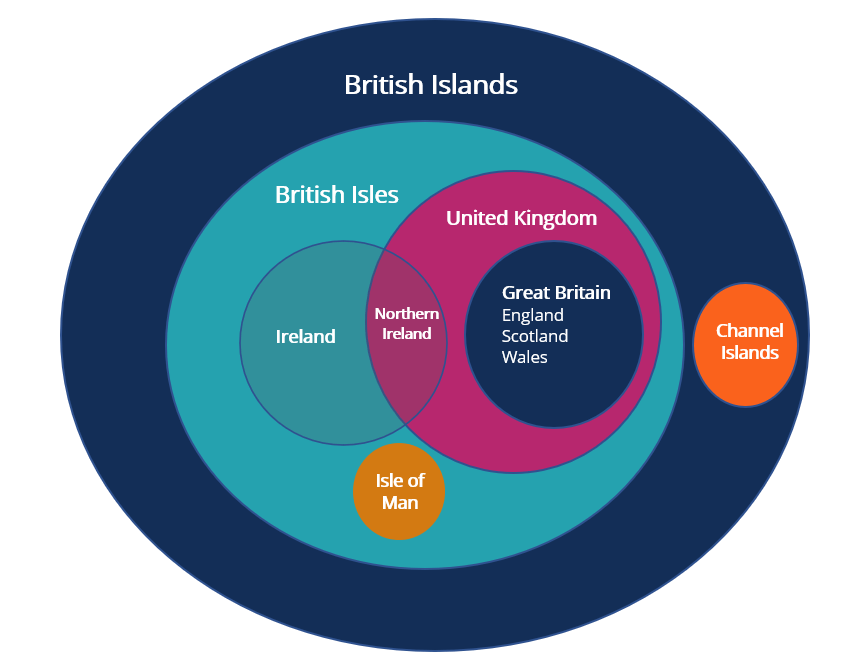
Cylinder Venn Diagrams

Venn diagrams do not just show overlaps but can also show subsets within a larger set or group. We illustrate below the British Islands, which clearly shows the subsets of each island from the larger set of British Islands.

Creating a Venn Diagram

A Venn diagram can be created in several ways. Below are various tools used to construct Venn diagrams:

• By using Shapes in Microsoft Office (Word, Excel, PowerPoint)
• By using SmartArt in Microsoft Office (Word, Excel, PowerPoint)
• By using online drawing tools such as canva, SmartDraw, visual-paradigm, visme, and creately, among others.

Benefits of Venn Diagrams

• Visual organization: Venn diagrams assist in the visual depiction of information, which helps students and professionals see the logic behind the relationships of particular elements.
• Assist in making decisions: Venn diagrams assist in making decisions between two or more choices. It makes it easier to compare and contrast. Hence, the use of Venn diagrams for assessment tends to generate discussions and provides information about participants’ thinking, which ultimately assists in decision-making.
• Reason through logic: Venn diagrams help to reason complex issues through logic. Mathematical problems can easily be reduced to a clear and understandable format.
• Detect data patterns: It is easier to detect data patterns that may not have been evident. Patterns such as probabilities and correlations are easily deduced.

Areas of Venn Diagram Application

• Set Theory: Set theory is a branch of mathematics where concepts of sets such as unions, intersection, and complements are found. It deals with extensive and complex problems that are solved using Venn diagrams.
• Logic: In logic, Venn diagrams are used to determine the validity of certain arguments and conclusions. It also employs deductive reasoning. They are useful in the practice of logic statements such as if/then, all/some/no, may be.
• Statistics and Probability: Venn diagrams are used in the field of statistics and probability, which deals with predicting the likelihood of an event occurring. They are strongly linked to predictive analysis.
• Teaching: Venn diagrams are also used in the teaching profession, particularly in the lower grades, to assist students’ reading comprehension. Students are able to understand concepts and explain similarities and differences between taught elements more clearly.
• Linguistics: Venn diagrams are also used in linguistics to show relationships between different languages. The evolution of languages overtime enables commonalities and differences among languages that developed from a common mother language.
• Business: In business, the application of Venn diagrams is varied. Many financial analysts and economists use Venn diagrams in presentations to clients, investors, suppliers, etc. They can be used to show relationships in products, processes, SBUs, ideas, and a host of other things.
• Computer Science: Application is done through visualizing programming languages and structures.

More Resources

Thank you for reading CFI’s guide to Venn Diagrams. To keep learning and developing your knowledge base, please explore the additional relevant resources below:

• Charts and Graphs Templates
• Dashboard Creation in Excel
• FinViz Financial Visualization Tools
• Excel Dashboards & Data Visualization Course
• See all business intelligence resources